The dynamics of neuronal assemblies in cortical networks based on excitatory and inhibitory balance
Neuronal assemblies are formed via the repetitive activation of subpopulations of neurons to guide learning and behavior. Technical advances have made it possible to artificially induce such assemblies, although the method of optimizing the various parameters remain to be identified. In a new report now published in Science Advances, Sadra Sadeh and Claudia Clopath at the Bioengineering department of the Imperial College London, U.K., studied this question in large-scale cortical networks with excitatory-inhibitory (E-I) balance. They identified the background network within which neuronal assemblies were embedded and how they strongly regulated their dynamics and formation. While networks with dominant excitatory interactions allowed the fast formation of neuronal assemblies, this process was accompanied by the recruitment of non-perturbed neurons for non-specific induction. Perturbation is a key technique in experimental systems neuroscience and can assist researchers establish how given neurons are causally related to a given behavior or to a succeeding neuronal activity. The results of this work highlighted the presence of two regions accompanying computational and cognitive tasks with speed and specificity.
Understanding the brain by studying neuronal assemblies
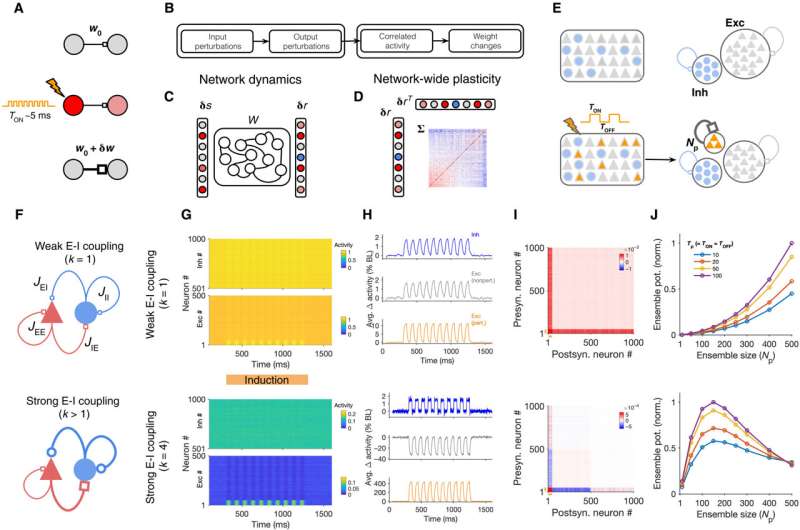
Neuronal assemblies or subgroups of interconnected, co-active neurons are the building blocks of computation and learning in the brain. With advancing technologies, scientists have gathered unprecedented tools to interact with the circuitry to record and perturb the activity of neuronal subpopulations and link their dynamic behavior. For instance, experimentalists can artificially induce neuronal assemblies by targeting the activation of a subset of cortical neurons and the efficient induction can provide a powerful method to trigger or suppress a behavior to guide the study of the human brain. Researchers aim to understand how the parameters of stimulation and the activation of neurons during perturbation techniques can be optimized for efficient induction. To study neuronal assemblies under biological conditions, researchers must assess the complex interplay of network dynamics and plasticity. In this work, Sadeh et al. studied how neuronal assemblies could be induced in large-scale recurrent networks of excitatory and inhibitory neurons under different conditions of perturbation. Using a theory developed recently to analyze the effect of neuronal perturbations, the team asked how activity changes resulting from different perturbations guided network-wide plasticity. In the first experimental step, they studied the transfer of input perturbations to output responses and analyzed the correlated activity patterns emerging from these responses to modify the neuronal assemblies.
Inducing neuronal assemblies in excitatory inhibitory networks
The research team then investigated the formation of neuronal assemblies by analyzing the different patterns of perturbations in large-scale cortical network models with balanced excitation and inhibition. Thereafter, they simulated the networks composed of these models using random recurrent connectivity. Sadeh et al. characterized the induction protocols based on key methods of the perturbations, including the number of targeted neurons and properties of the stimulus. Next, they simulated the response of the network before and after perturbations in each regime to show the dominance of excitatory recurrent interactions for non-perturbed excitatory neurons during weak excitation-inhibition coupling. In contrast, nonperturbed excitatory neurons in networks with strong excitatory-inhibitory coupling showed dominance of inhibitory recurrent interactions, where both effects were stronger when increasing the size of the perturbed ensemble in the study.
Transactions in cortical networks
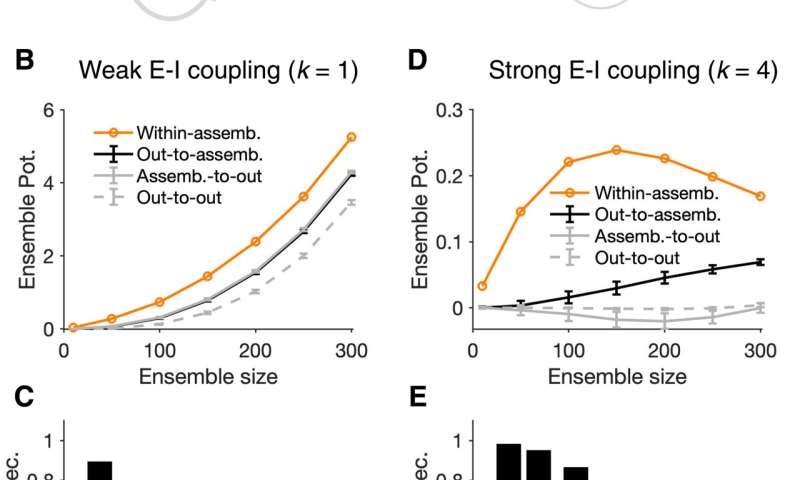
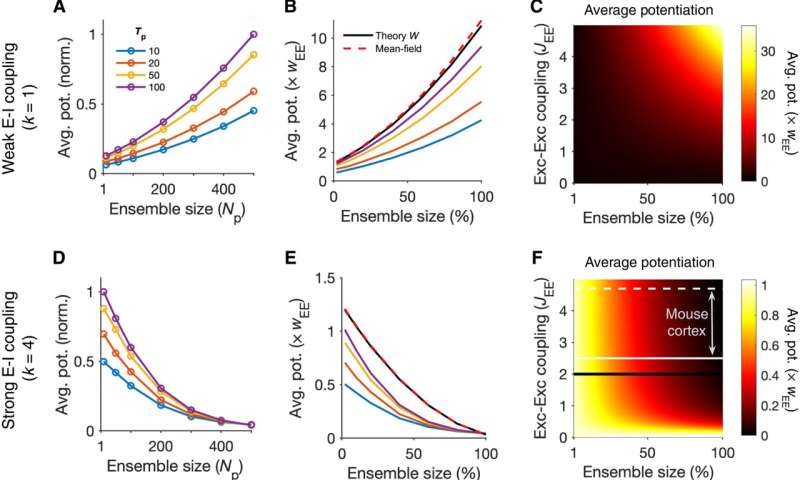
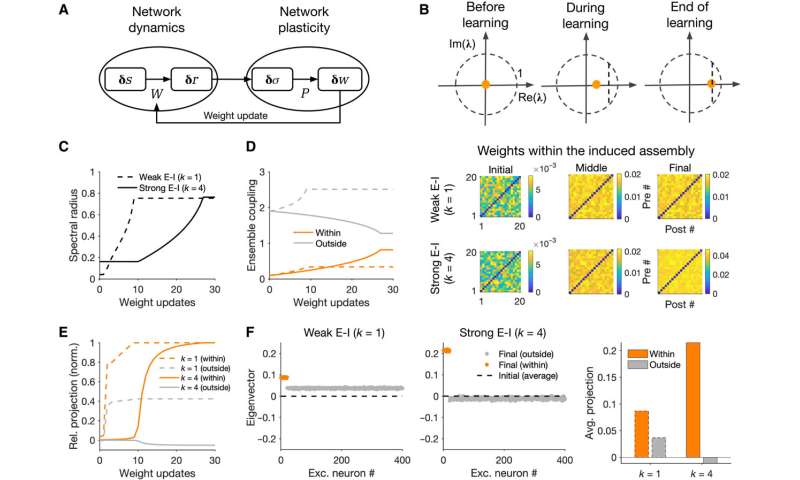
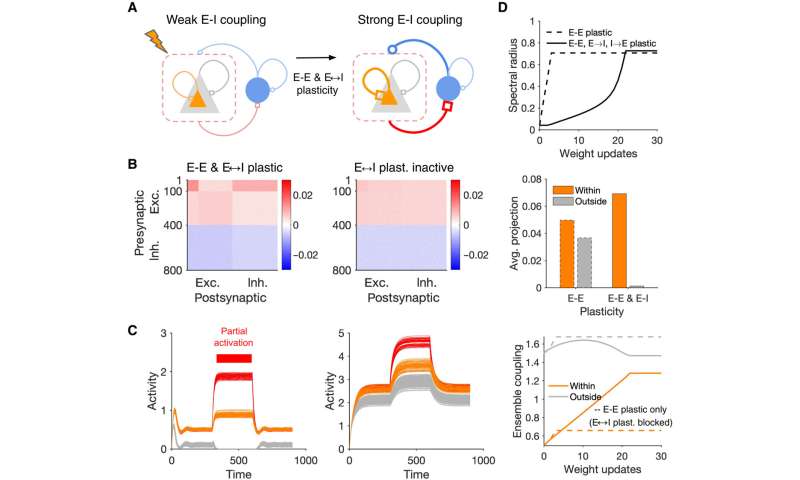
To further understand the formation of assemblies in diverse regions, Sadeh et al. studied how the average strength of individual synapses changed as a function of parameters of perturbation. In the ensemble of perturbed neurons, they plotted the average potentiation of synapses for different regions and showed how cooperativity during the formation of neuronal assemblies emerged in networks with weaker E-I (excitatory-inhibitory) coupling. This changed to suppressive effects in networks with stronger interactions. Pre-existing wiring in the network guided the process and connections between neurons could be organized according to their functional properties. Cortical networks could typically regulate their activity after sensory deprivation such as injury or input deprivation, where neuronal assemblies were involved during subnetwork-specific recovery. To understand this process, Sadeh et a. reduced the feedforward input to a compartment of neurons in the network and studied how correlated external activation of a subset led to recovery. The results showed how strong E-I (excitatory-inhibitory) interactions shaped the formation of specific neuronal assemblies in the network and their recovery consequent to input deprivation.
Behavioral performances associated with neuronal assemblies
Neuronal assemblies are also associated with different stimuli to guide and trigger behavior. Sadeh et al. next sought to understand how neuronal assemblies formed in different E-I regions contributed to behavioral performance by simulating the development of two neuronal assemblies associated with distinct stimuli. Networks with weak E-I coupling swiftly increased in recall strength to represent the capacity of the network to detect the presence of a stimulus. Based on the outcomes, neuronal assemblies amplified a weak stimulation of a small fraction of their neurons to provide a substrate for fast and strong recalls. In networks with strong E-I coupling, the recall strength was comparatively weaker, rising up more slowly. The results highlighted the slower emergence of neuronal assemblies in inhibition-dominated regions, while comparatively, the assemblies formed in weaker E-I regions were fit for faster, yet more crude cognitive tasks. The researchers showed how they can regulate different modes of learning by modulating the E-I balance in the network via top-down mechanisms to provide a powerful method. The team achieved different modes of learning and induction, by generally modulating the network followed by studies on dynamic transitions between different regions of excitatory-inhibitory (E-I) plasticity to show how different plasticity rules shaped the dynamics of learning in different manners.
Outlook
Source: Read Full Article